이번 포스팅은 Binary Search(이진 탐색)에 대한 기록입니다.
이진 탐색 알고리즘은 배열과 Target을 가지고 특정 값의 위치를 찾는 알고리즘입니다.
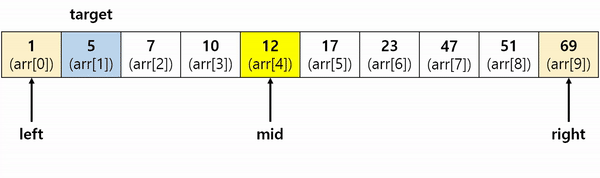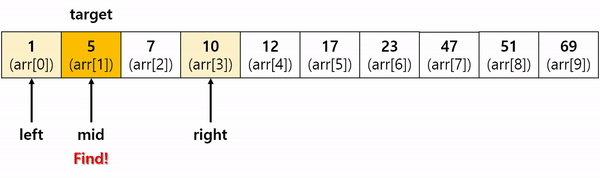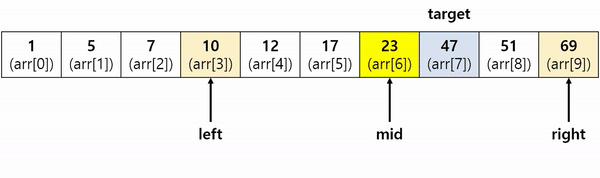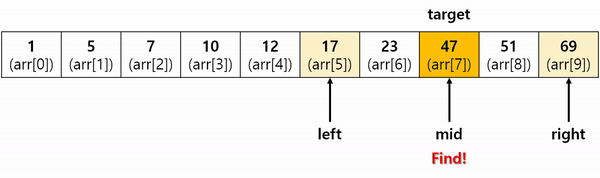
주어진 배열의 시작점, 끝점을 기준으로 정 가운데 값과 Target 값을 비교하며 같은 값이 나올 때까지 시작점, 끝점의 범위를 대폭 좁혀가며 Target의 위치값을 찾는 것이 이 알고리즘의 핵심입니다.
사람이 사전에서 특정 단어를 찾기 위해 앞 뒤 페이지를 뒤지는 것과 유사한 원리입니다.
이 과정을 그림으로 표현한 것이 상단에 있는 이미지입니다.
이 알고리즘을 적용하기 위해서는 주어지는 값이 반드시 오름차순 정렬된 상태여만 합니다.
따라서 정렬되지 않은 데이터 묶음에 대해서는 적용하기 어려운 알고리즘입니다.
아래의 코드는 Python으로 작성된 예제입니다.
#-*-encoding:utf-*-
def binarySearch(target, arr):
arr.sort()
left = 0 #배열의 왼쪽 위치
right = len(arr) -1 #배열의 오른쪽 위치(배열의 가장 끝)
while left <= right:
# 중간지점 값을 산출, 소수점은 버린다.
mid = (left + right) // 2
# 일치하는 값이 있다면 위치 반환
if arr[mid] == target :
return mid
#타겟이 mid보다 크므로 왼쪽 위치값을 좁힌다.
elif arr[mid] < target :
left = mid + 1
#타겟이 mid보다 작으므로 오른쪽 위치값을 좁힌다.
else:
right = mid - 1
if __name__ == "__main__":
arr = [1,5,7,10,12,17,23,47,51,69]
target = 17
result = binarySearch(target,arr)
print('Target의 값:', target, ' | 위치 값: ', result)
위 코드의 결과 값은 다음과 같습니다.


배열을 정렬했을 때 17의 위치는 배열주소 5번에 위치하므로 올바른 결과값을 도출했습니다.
'Dev > Algorithm' 카테고리의 다른 글
| [Algorithm] 선택, 삽입, 버블 정렬 (0) | 2021.04.24 |
|---|---|
| [Algorithm] 에라토스테네스의 체 (0) | 2021.04.24 |
| [Algorithm] 정렬 - 가장 큰 수 (0) | 2020.08.20 |
| [Algorithm] 정렬 - K번째 수 (0) | 2020.08.17 |


