저는 학창 시절 배웠던 교과목 중 제일 흥미를 가지지 못했던 과목이 수학입니다.
성적도 다른 과목에 비해 제일 낮았고 소위 말하는 수포자였죠.
그런 와중에 프로그래머를 업으로 시작하고 현재에 이르러서 수학적 지식의 필요성을 느껴 뒤늦게 다시 수학책을 펼쳐보고 있습니다.
(중학교 수학 지식 조차 잊어버려 지금은 상당히 애를 먹고 있습니다.)
공부하던 중 에라토스테네스의 체라는 소수를 걸러내는 알고리즘을 알게 되었습니다.
소수란 1과 자기 자신 외에 다른 약수가 없는 수를 뜻합니다.
이를 걸러내는 방법으로는 에라토스테네스의 체가 흔히 쓰인다고 합니다.
에라토스테네스의 체는 여러 숫자들 중 체로 치듯 걸러서 소수만 남기는 방법으로 과정은 아래와 같습니다.
1. 찾을 범위까지의 수를 나열하고, 소수가 아닌 1을 먼저 지운다.
2. 1 다음으로 큰 수인 2를 남겨두고 2의 배수를 모두 찾아서 지운다.
3. 그다음으로 큰 수이면서 지워지지 않을 3을 남겨두고 3의 배수를 모두 지운다.
4. 더 이상 지울 수 있는 것이 없을 때까지 반복한다.
위 과정을 봤을 때, 프로그래밍 코드로 구현이 가능하다 생각되어 여기저기서 자료를 참고해 나름대로 구현해보았습니다.
거두절미하고 우선 파이썬으로 작성한 코드부터 보겠습니다.
import math
def prime(num):
# 에라토스테네스의 체
# 입력된 수 까지 전체 수를 나열
array = [i for i in range(num + 1)]
# 제곱근: 입력된 수의 최소 소수는 제곱근 이하의 값에서 성립된다.
sqrt = int(math.sqrt(num))
for i in range(2, sqrt + 1):
"""
소수의 자격은 2 이상부터 성립되므로 시작 범위를 i = (2 ~ 제곱근)으로 한다.
i 범위에서 각배수 값 j에 해당하는 각 위치의 값을 0으로 치환한다.
j는 2배수, 3배수, ... 의 값을 걸러내기 위해 사용된다.
"""
j = 2
while i * j <= num and (i * j) < len(array):
array[i * j] = 0
j += 1 # 2 * 2, 2 * 3, ... 배수에 해당하는 값들을 순회하며 값을 0으로 치환
# 0, 1은 소수에 포함되지 않으므로 그보다 큰 숫자들만 걸러서 반환한다.
return [i for i in array if i > 1]
if __name__ == '__main__':
prime_array = prime(25)
print(prime_array)
위 알고리즘 4단계 과정을 코드로 옮길 때에 약간의 순서 조정이 필요했습니다.
for문과 list를 이용해서 전체 수를 쭉 훑어가며 문제를 해결해야 하는데, 먼저 1을 지워버리면 배열의 위치 값을 찾는데 꽤나 복잡해 지기 때문에 우선 저는 0, 1을 남겨둔 상태를 전제로 이를 해결해보고자 했습니다.
array로 0부터 최대 숫자까지 일단 숫자를 쭉 나열합니다.
그다음, 제곱근을 가져오는데, 이는 나열된 숫자들의 최대 수의 (예시에서는 0 ~ 25) 제곱근 √25 = 5의 범위 내의 배수들만 지우는 것으로도 배열 내 존재하는 소수들을 남길 수 있기 때문입니다.
정확히는 2 이상의 숫자만이 소수의 자격을 가질 수 있는 조건이 되기 때문에 2 ~5 사이의 범위가 해당되겠습니다.
(제곱근은 전체 배열의 최대 숫자에 따라 다르게 출력됩니다. 예) √100 = 10 )
변수 i 값을 이용해 제곱근 범위를 순회합니다.
그리고 while문과 j 값을 이용해 2 배수, 3 배수, ... 배수를 늘려가며 해당하는 list의 인덱스 값을 0으로 우선 치환합니다.
while문이 한 번 돌 때마다 배수가 늘어납니다.
이때 1 배수부터 시작하지 않는 이유는 2, 3 등 최소 단위 소수를 남겨둬야 하기 때문입니다.
위 while 과정에서 찾아낸 배수들을 바로 지우는 것이 아닌 0으로 치환하는 것은 다른 검사해야 할 값의 위치 값을 유지시키기 위함입니다.
그리고 배수 값 j를 계속 늘려가게 된다면 언젠가는 주어진 array의 범위를 초과하기 때문에 이를 방지하기 위해 i * j 값이 배열을 넘어가지 않도록 (i * j) < len(array) 조건을 추가해 줍니다.
모든 소수를 걸러 냈다면 연산된 데이터는 다음과 같이 바뀝니다.
[0, 1, 2, 3, 0, 5, 0, 7, 0, 0, 0, 11, 0, 13, 0, 0, 0, 17, 0, 19, 0, 0, 0, 23, 0, 0]소수가 아닌 값이 있던 자리가 0으로 바뀌고, 소수에 해당하지 않는 1도 남아있는 것을 확인할 수 있습니다.
여기서 배열의 숫자를 n이라고 두었을 때 n > 1 조건으로 치환된 값과 1을 최종적으로 걸러내주면 아래와 같은 형태로 값이 정돈되게 됩니다.
array = [i for i in array if i > 1]
array = [2, 3, 5, 7, 11, 13, 17, 19, 23]
위 과정을 조금 더 직관적으로 표현하자면 아래의 표와 같습니다.
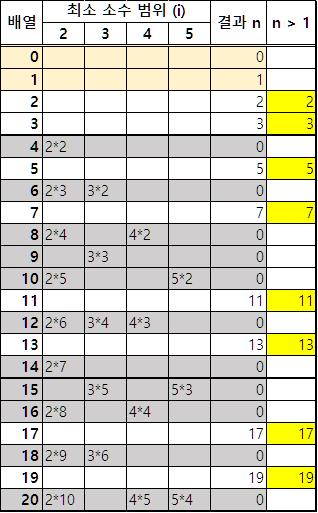
참고로 위 알고리즘은 프로그래머스 코딩 테스트 연습문제에도 출제가 되어있습니다.
programmers.co.kr/learn/courses/30/lessons/12921?language=python3
코딩테스트 연습 - 소수 찾기
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요. 소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다. (1은 소수가 아닙니다.) 제한 조건 n은 2이상
programmers.co.kr
위 사이트에서 본 포스팅의 알고리즘은 아래와 같은 평가를 받았습니다.

에라토스테네스의 체는 가장 효율적인 알고리즘으로 작성되었을 때 O(n)의 시간 복잡도를 가진 다고 합니다.
독자분들도 다양한 방법을 사용해 보다 효율적인 시간 복잡도를 가진 에라토스테네스의 체를 구현해 보시길 바랍니다.
이것으로 에라토스테네스의 체 알고리즘 포스팅을 마치겠습니다.
'Dev > Algorithm' 카테고리의 다른 글
| [Algorithm] 선택, 삽입, 버블 정렬 (0) | 2021.04.24 |
|---|---|
| [Algorithm] Binary Search(이진 탐색) (0) | 2020.09.17 |
| [Algorithm] 정렬 - 가장 큰 수 (0) | 2020.08.20 |
| [Algorithm] 정렬 - K번째 수 (0) | 2020.08.17 |


